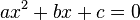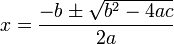kengjang

สมการกำลังสาม

สมการกำลังสาม
ในทางคณิตศาสตร์ สมการกำลังสาม คือสมการของพหุนามตัวแปรเดียวที่มีดีกรีเท่ากับ 3 รูปแบบทั่วไปของสมการกำลังสามคือ

$ax^3 + bx^2 + cx + d = 0 \!$

สูตรกำลังสาม
ถ้าหาก

x 1, x 2, x 3

เป็นคำตอบของสมการกำลังสามแล้ว เราจะสามารถแยกตัวประกอบของพหุนามกำลังสามได้ดังนี้

$ax^3 + bx^2 + cx + d = a(x - x_1)(x - x_2)(x - x_3) = 0 \!$

กำหนดให้

$\begin{align} q &= \frac{9abc - 27a^2d - 2b^3}{54a^3} \\ r &= \sqrt{\left (\frac{3ac-b^2}{9a^2}\right )^3 + q^2} \\ s &= \sqrt[3]{q + r} \\ t &= \sqrt[3]{q - r} \\ \end{align}$

คำตอบของสมการทั้งสามค่าสามารถคำนวณได้จากสูตร

$\begin{align} x_1 &= s+t-\frac{b}{3a} \\ x_2 &= -\frac{1}{2}(s+t)-\frac{b}{3a}+\frac{\sqrt{3}}{2}(s-t)i \\ x_3 &= -\frac{1}{2}(s+t)-\frac{b}{3a}-\frac{\sqrt{3}}{2}(s-t)i \\ \end{align}$

เมื่อ i คือหน่วยจินตภาพที่นิยามโดย i² = −1

สมการกำลังสอง

สมการกำลังสอง

ในทางคณิตศาสตร์ สมการกำลังสอง (สมการควอดราติก) คือสมการของพหุนามตัวแปรเดียวที่มีดีกรีเท่ากับ 2 รูปแบบทั่วไปของสมการกำลังสองคือ

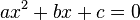
$ax^2 + bx + c = 0 \!$

สูตรกำลังสอง
สมการกำลังสองใดๆ ที่มีสัมประสิทธิ์เป็นจำนวนจริง (หรือจำนวนเชิงซ้อน) จะมีรากของสมการ 2 คำตอบเสมอ ซึ่งอาจจะเท่ากันก็ได้ โดยที่รากของสมการสามารถเป็นได้ทั้งจำนวนจริงหรือจำนวนเชิงซ้อน สามารถคำนวณได้จากสูตร

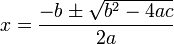
$x = \frac{-b \pm \sqrt {b^2-4ac}}{2a}$

ซึ่งเครื่องหมายบวกและลบเป็นการแทนความหมายของทั้งสองคำตอบ ได้แก่

$x_+ = \frac{-b + \sqrt {b^2-4ac}}{2a}; \quad x_- = \frac{-b - \sqrt {b^2-4ac}}{2a}$

ดังนั้นค่าของสมการจะเท่ากับฟิวชั่นของสมการ

กราฟของคู่อันดับ

ตำแหน่งของจุด A คือ (1,2)
ตำแหน่งของจุด B คือ (-2,3)
ตำแหน่งของจุด C คือ (-3,-2)
ตำแหน่งของจุด D คือ (2,-4)
เรียกจุดที่แทนตำแหน่งคู่อันดับว่ากราฟของคู่อันดับและเรียก ตำแหน่งของคู่อันดับว่าพิกัด

ตัวอย่างที่ 1 จงเขียนกราฟของจุด (1,5), (2,-3), (-3,-2), (4,-1)
วิธีทำ

graph2

สำหรับแกนนอนโดยทั่วไปจะแทนด้วยแกน x และแกนตั้งโดยทั่วไปจะแทนด้วยแกน y ดังรูป

graph3

แกน x และแกน y ตัดกันเป็นมุมฉากเรียกจุดที่แกน x แกน y ตัดกันว่า จุดกำเนิดและแกน x กับแกน y จะแบ่งพื้นที่ซึ่งพื้นที่นี้เรียกว่าระนาบออกเป็น 4 ส่วน แต่ละส่วนเรียกว่าจตุภาพ ซึ่งเขียนแทนแต่ละจตุภาคดังนี้

graph

ตัวอย่างที่ 2 จงเขียนจุด A, B, C, D, E, F ลงในแต่ละจตุภาค เมื่อจุด A, B, C, D, E, และ F มีพิกัดดังนี้
                      (4,3), (-6,2), (-4,-1), (-5,4), (2,6), (3,-6) ตามลำดับ
วิธีทำ

   graph5

ตัวอย่างที่ 3 กำหนด A(-4,6), B(3,-5), C(2,2), D(-1,-2), จุด A, B, C, D, อยู่ในจตุภาคใด
graph6

วิธีทำ จุด A(-4,6) อยู่ในจตุภาคที่ 2
จุด B(3,-5) อยู่ในจตุภาคที่ 4
จุด C(2,2) อยู่ในจตุภาคที่ 1
จุด D(-1,-2), อยู่ในจตุภาคที่ 3

ตัวอย่างที่ 4 A, B, C, D เป็นจุดยอดของสี่เหลี่ยมจัตุรัส ถ้าจุด A, B อยู่ในจตุภาคที่ 1 และ 2 ตามลำดับ และ C มีพิกัด (-3,-5) และ D มีพิกัด (4,-5) จงหาพิกัดของจุด A และ จุด B

วิธีทำ

ดังนั้นจุด A มีพิกัด (4,2) และจุด B มีพิกัด (-3,2)

วันพฤหัสบดีที่ 12 มกราคม พ.ศ. 2555

สมการกำลังสาม

สมการกำลังสอง

กราฟของคู่อันดับ

กราฟของคู่อันดับ